Giovanni Dematteis

Giovanni Dematteis

My research aims at quantifying the energy transfer and localization pathways in systems of random waves, with a focus on problems of Physical Oceanography

  • Physical Oceanography
  • Wave Turbulence
  • Statistical Physics
  • Extreme Events

Research

Energy fluxes in the oceanic internal wave field

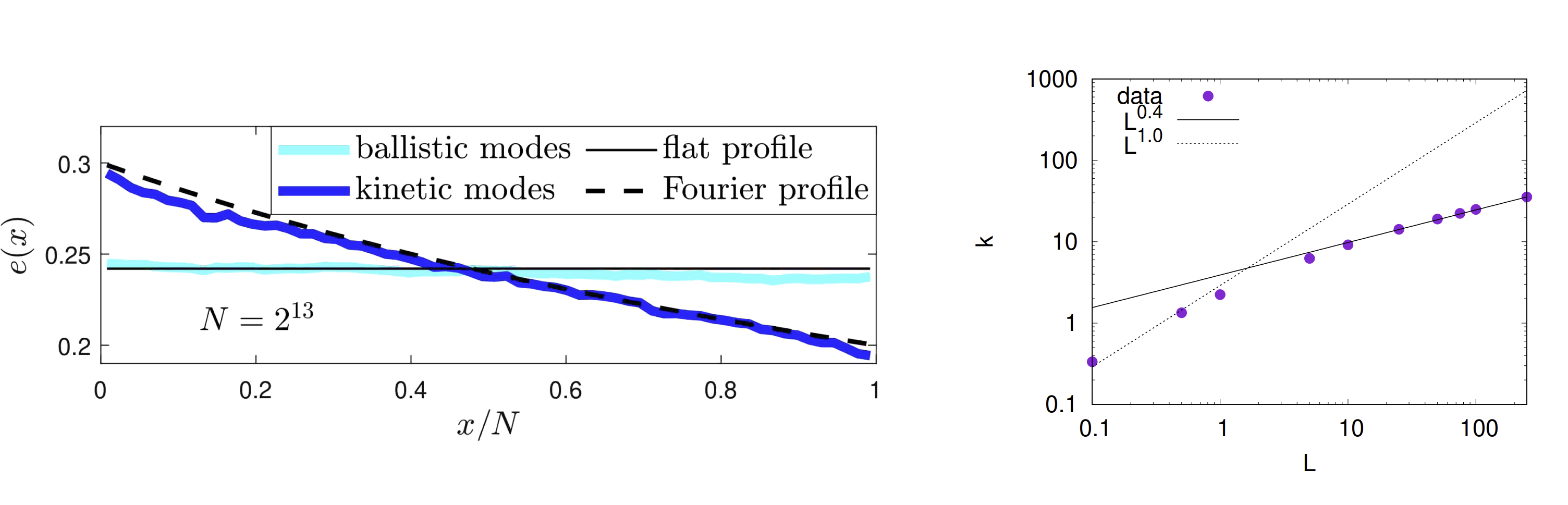
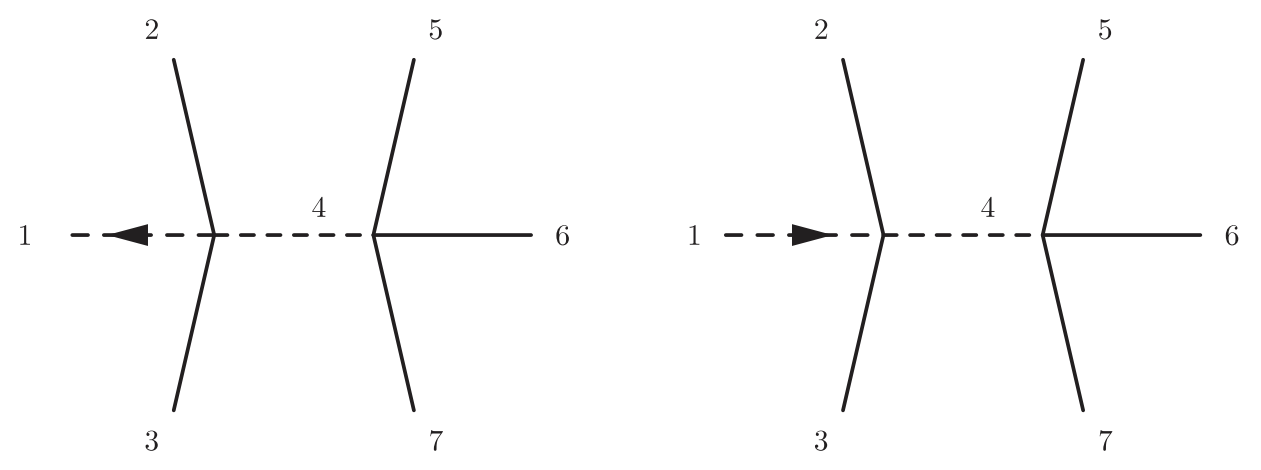
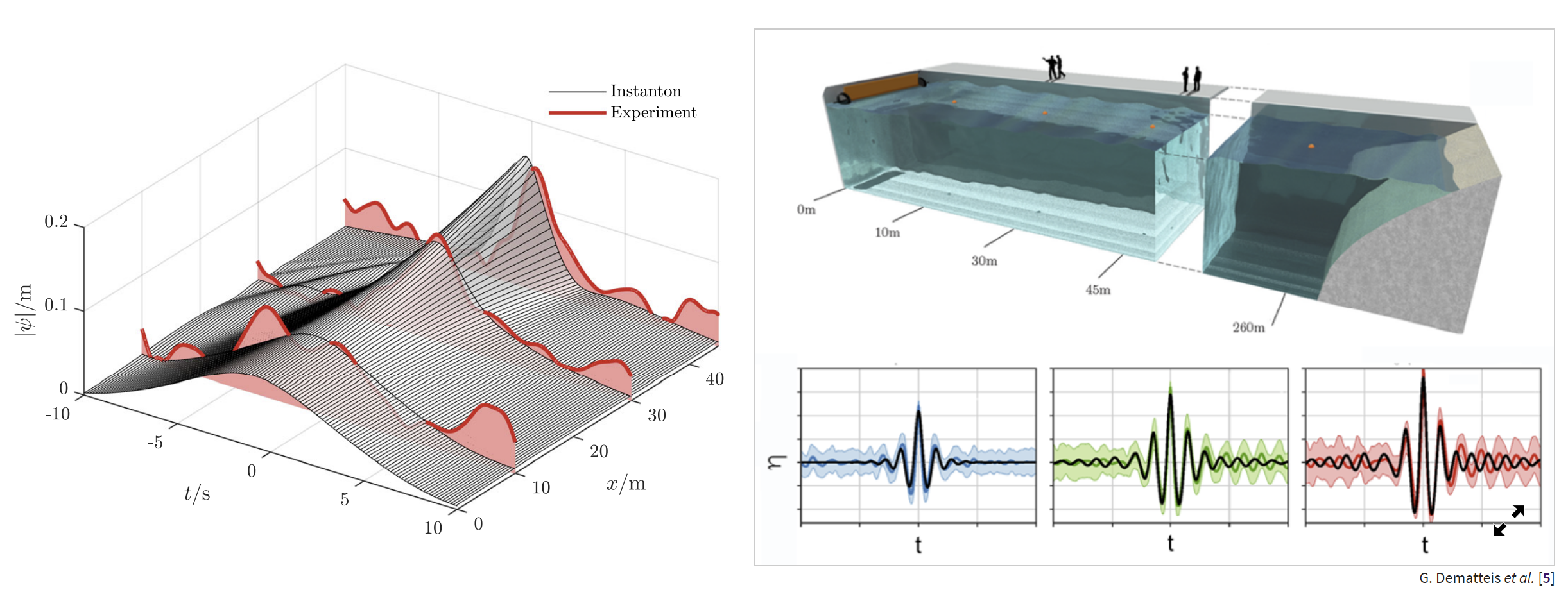
The rate of diapycnal mixing, largely due to internal-wave breaking, is a key ingredient to understanding upwelling and horizontal circulation in the abyssal ocean. We work on developing a first-principles analysis of the downscale energy flux in the internal wave field, with the aim of providing a solid theoretical background to the finescale parameterizations that are used to include the effects of internal waves in the Global Circulation Models.

Thermal transport in particle lattices

The theory of interacting waves finds ubiquitous application in nature, from the planetary scales down to the scales of a millimeter-long carbon nanotube, where thermal conduction is due to interactions of reticular oscillations known as phonons. I have conducted recent investigations that are shedding new light on the anomalous thermal conduction properties of low-dimensional particle lattices.

Wave Turbulence Theory derivations

The field has been devoted increasing attention in the past fiew years in the effort to prove rigorously the validity of the wave kinetic equation, which describes the energy transfers between different scales in wave systems, via nonlinear resonant interaction. Since my MSc thesis, I have worked on derivations in wave kinetic theory using diagrammatic techniques, obtaining original results on the preservation of chaos for four-wave systems.

Large deviations and extreme events

During my PhD I have developed a method based on large deviation theory and numerical optimization in order to explain the formation of oceanic rogue waves. The resulting method for extreme events that we have formalized paves the way for applications of large deviation theory in wave systems and in generic deterministic systems supplemented with random initial conditions and/or parameters. This project resulted in publications in PNAS and PRX, and was featured in popular science venues such as Scientific American, Quanta Magazine and the Physics magazine of the APS.